Introduction

Back in 1931, a young mathematician named Kurt Gödel dropped what might be the biggest bombshell in the history of mathematics. And here’s the crazy part - what he discovered about math ended up being crucial for understanding why some programming problems are just… impossible to solve.

You know how we developers always want to build the “perfect” system? Well, Gödel basically proved that perfection is mathematically impossible. Not just hard - literally impossible. And this isn’t just some abstract math theory - it directly explains why we can’t solve the halting problem, why some algorithms will always be approximations, and why that “universal AI” everyone talks about can’t exist.

Let me break this down in a way that actually makes sense for us.

So What Did Gödel Actually Prove?

Gödel’s theorem comes in two parts, and both are mind-bending:

First Theorem: There Are Always True Things You Can’t Prove

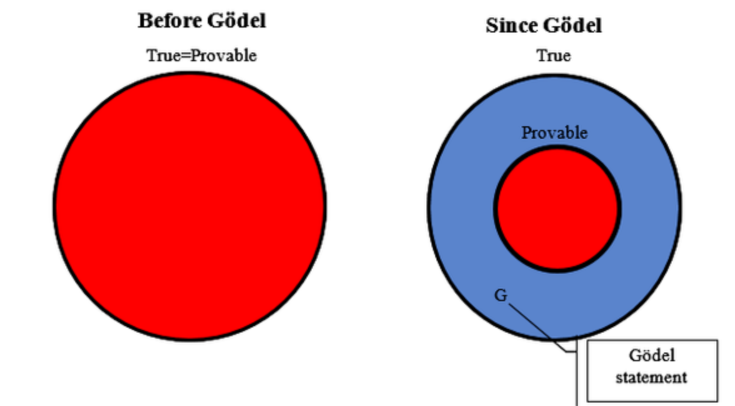
If you have any mathematical system that can do basic arithmetic (like 2+2=4), there will always be true statements that the system simply cannot prove. It’s not that we haven’t found the proof yet - the proof literally cannot exist within that system.

Think of it like this: no matter how comprehensive your test suite is, there are always bugs you’ll never catch.

Second Theorem: You Can’t Prove You’re Bug-Free

A system cannot prove that it’s consistent (bug-free) using only its own rules. It’s like trying to debug your own code without any external tools - you might miss your own logical blind spots.

The “Aha!” Moment

Here’s the clever trick Gödel used. He basically created a mathematical statement that says: “This statement cannot be proven.”

Now think about it:

• If you can prove it, then the statement is false (but you just proved it’s true - contradiction!)
• If you can’t prove it, then the statement is true (but unprovable)

It’s like a mathematical catch-22. Gödel found a way to create these paradoxes inside any sufficiently complex mathematical system.

A Developer’s Analogy

Imagine you’re trying to write the ultimate code style guide that covers every possible coding situation and never contradicts itself. Gödel basically proved this is impossible - there will always be edge cases your guide can’t handle, or rules that conflict with each other. The more comprehensive you try to make it, the more contradictions you’ll find.

The Core Insight

Gödel used a clever encoding scheme where mathematical statements could be represented as numbers, then constructed a statement that essentially says “I cannot be proven.” This creates a logical paradox that reveals fundamental limits in any sufficiently complex system.

Why This Matters for Developers

The Halting Problem - Or “Why We Can’t Have Nice Things”

Remember that function you always wished existed - one that could tell you if any program will eventually finish running or get stuck in an infinite loop? Turns out, Gödel’s work explains why this is impossible.

If such a function existed, we could create the same type of paradox Gödel discovered: a program that does the opposite of what the halting function predicts, creating a logical contradiction.

This isn’t just academic - it means there are fundamental questions about code that no algorithm can ever answer universally.

Problems That Just Can’t Be Solved

Gödel’s insights revealed that some problems are undecidable - not “really hard to solve,” but literally impossible for any algorithm to solve in all cases. Examples include determining if two programs are equivalent, or whether a program will produce a specific output.

Think of it like a hierarchy of difficulty:

• P problems: Easy (polynomial time)
• NP problems: Hard to solve, easy to verify
• PSPACE, EXPTIME: Really hard
• Undecidable: Impossible (thanks, Gödel!)

Why “Provably Correct” Software Is Tricky

When we try to formally verify software (prove it’s correct), Gödel’s limitations come back to haunt us:

class FormalVerification:
    """
    Formal verification must work within Gödel's limitations
    """

    def verify_program_correctness(self, program, specification):
        """
        Attempt to prove program correctness
        Limited by incompleteness theorem
        """
        # We can verify specific properties, but not all possible properties
        # Some true facts about the program may be unprovable

        verifiable_properties = [
            "termination_in_specific_cases",
            "memory_safety_bounds",
            "type_correctness"
        ]

        # But we cannot prove: "This program is correct for ALL inputs"
        # without potentially missing some true but unprovable properties

        return self._partial_verification(program, specification)

    def _partial_verification(self, program, spec):
        # Verification within known limitations
        pass

What This Means for Software Engineers

Embracing “Good Enough” Solutions

Instead of chasing perfect algorithms, modern software engineering embraces:

• Heuristic approaches when exact solutions are impossible
• Approximation algorithms that get “close enough” efficiently
• Machine learning models that learn patterns rather than prove theorems
• Bounded verification that checks what we can within reasonable limits

Probabilistic Thinking

When certainty is impossible, we use probabilistic methods:

• A/B testing to make decisions with statistical confidence
• Load balancing that distributes traffic probabilistically
• Caching strategies that work well most of the time
• Security measures that make attacks computationally impractical, not impossible

Modern Applications and Examples

Machine Learning and AI

Gödel’s theorems influence AI by highlighting fundamental limitations. No universal learning algorithm can optimally solve all problems (related to the “No Free Lunch” theorem), and AI systems cannot prove their own consistency due to the second incompleteness theorem.

Cryptography and Security

Cryptographic security relies on computationally hard problems like factoring and discrete logarithms. While these seem difficult, we cannot formally prove their hardness - a limitation connected to Gödel’s insights about the boundaries of mathematical proof.

Database Systems

Database query optimization is undecidable in general, forcing systems to use heuristics. Similarly, verifying all possible consistency constraints is impossible - databases can only check specific, known constraints within computational limits.

Philosophical Implications for Computer Science

The Limits of Formal Methods

Gödel’s theorems teach us humility about what we can prove. Perfect software verification has fundamental limitations - some true properties cannot be proven, and we cannot prove our verification systems are sound. This leads to practical approaches like bounded verification, empirical testing, and type systems.

Embracing Uncertainty

Modern computer science embraces probabilistic and approximate solutions. We use Monte Carlo methods, probabilistic data structures (Bloom filters, HyperLogLog), and machine learning models that quantify their own uncertainty rather than claiming absolute truth.

Practical Guidelines for Developers

Design with Limitations in Mind

Build systems that gracefully handle incompleteness through fail-safe design, empirical monitoring, redundancy, bounded guarantees, and human oversight. Expect unexpected failure modes and use timeouts, circuit breakers, and graceful degradation.

Testing and Validation Strategies

Since we cannot test all possible behaviors, focus on critical paths using unit tests, integration tests, property-based testing, fuzzing, production monitoring, and chaos engineering. Acknowledge that testing has limits and prioritize accordingly.

Contemporary Research and Developments

Automated Theorem Proving

Modern systems like Coq, Lean, and Isabelle work within Gödelian limitations by requiring human guidance. They cannot automatically prove all true statements but excel at verifying human-constructed proofs and working within decidable fragments.

Quantum Computing

Even quantum computing doesn’t escape Gödel’s limitations. While quantum algorithms like Grover’s search and Shor’s factoring provide speedups for specific problems, undecidable problems remain unsolvable even in the quantum realm.

Conclusion

Gödel’s Incompleteness Theorem stands as one of the most profound results in mathematics and logic, with far-reaching implications for computer science and algorithm design. Rather than being a limitation to overcome, incompleteness is a fundamental feature of sufficiently complex formal systems—including the computational systems we build every day.

Key Takeaways for Computer Scientists

1. Embrace Limitations: Perfect, complete solutions are often impossible. Design systems that work well within known constraints.

2. Use Probabilistic Approaches: When deterministic completeness is unattainable, probabilistic and approximate methods often provide practical solutions.

3. Value Empirical Validation: Since we cannot prove all true statements about our systems, empirical testing and monitoring become crucial.

4. Design for Uncertainty: Build systems that gracefully handle unexpected situations and partial information.

5. Combine Formal and Informal Methods: Use formal verification where possible, but supplement with testing, monitoring, and human judgment.

The Deeper Message

Gödel’s theorem teaches us humility in the face of complexity. It reminds us that there are fundamental questions that no algorithm can answer, fundamental limits to what we can prove, and fundamental uncertainties we must learn to navigate.

Yet this is not a message of despair—it’s a call to be more thoughtful, more empirical, and more creative in our approach to computational problems. Some of computer science’s greatest advances, from probabilistic algorithms to machine learning to interactive proof systems, can be seen as successful strategies for working within and around the boundaries that Gödel revealed.

In the end, Gödel’s Incompleteness Theorem doesn’t close doors—it opens them to new ways of thinking about computation, proof, and the beautiful complexity of the systems we create.

So next time you’re debugging a particularly stubborn piece of code or wondering why that “perfect” algorithm doesn’t exist, remember Gödel. Sometimes the most profound insights come from understanding our limitations rather than pretending they don’t exist.

Keep building, keep questioning, and remember - even math has bugs that can’t be fixed.

Until next time! 👨‍💻